Çarpma Kuralı

Ayrık iki tane işlemden birinci işlem değişik yoldan, ikinci işlem değişik yoldan gerçekleştirilebiliyorsa, bu iki tane işlem birlikte (1. si ve 2. si)

değişik yoldan gerçekleştirilebilir ve bu şekildeki sayma işlemine genel çarpım kuralı veya saymanın temel kuralı denir.

Bir sınıfta 6 erkek ve 5 kız öğrenci vardır.
Buna göre, bu sınıftan 1 erkek ve 1 kız öğrenci kaç farklı şekilde seçilir?
A) 5 B) 6 C) 11 D)15 E) 30

6 erkek öğrenci arasından 1 erkek öğrenci 6 farklı şekilde, 5 kız öğrenci arasından 1 kız öğrenci 5 farklı şekilde seçilir.
Buna göre, 1 erkek ve 1 kız öğrenci 6.5= 30 farklı şekilde seçilir.
Yanıt E

Bir öğrencinin farklı 3 defteri, farklı 4 kalemi ve farklı 3 silgisi vardır.
Buna göre, bu öğrenci 1 defteri, 1 kalemi ve 1 silgiyi kaç farklı şekilde seçebilir?
A) 10 B) 12 C) 18 D) 36 E) 72

Farklı 3 defter arasından 1 defter 3 farklı şekilde, farklı 4 kalem arasından 1 kalem 4 farklı şekilde, farklı 3 silgi arasından 1 silgi 3 farklı şekilde seçilir.
Buna göre, bu öğrenci 1 defter, 1 kalem ve 1 silgiyi 3.4.3 = 36 farklı şekilde seçilebilir.
Yanıt D

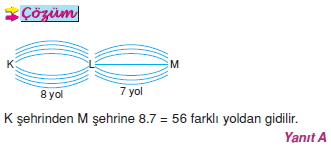
K şehrinden L şehrine 8 farklı yol ve L şehrinden M şehrine 7 farklı yol vardır.
Buna göre, L şehrine uğramak şartıyla K şehrinden M şehrine kaç farklı yoldan gidilir?
A) 56 B) 36 C) 28 D) 15 E) 14

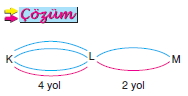
K şehrinden L şehrine 4 farklı yol ve L şehrinden M şehrine 2 farklı yol vardır.
Buna göre, L şehrine uğramak şartıyla K şehrinden M şehrine gidilen yol bir daha kullanılmamak üzere,
kaç farklı yoldan gidilip dönülür?
A) 12 B) 24 C) 32 D) 48 E) 64

K şehrinden L şehrine 4 farklı yol, L şehrinden M şehrine 2 farklı yol olduğundan, K şehrinden M şehrine 4.2 farklı yoldan gidilir.

Dönüşte gidilen yol kullanılmayacağına göre, M şehrinden, L şehrine 1 farklı yol, L şehrinden K şehrine 3 farklı yol olduğundan, M şehrinden K şehrine 1. 3 farklı yoldan dönülür.

Buna göre, K şehrinden M şehrine gidilen yol bir daha kullanılmamak şartıyla,
4.2.1.3 = 24 farklı yoldan gidilip dönülür.
Yanıt B

20 kişilik bir sınıftan 1 başkan ve 1 başkan yardımcısı kaç farklı şekilde seçilir?
A) 400 B) 380 C) 80 D) 40 E) 20

20 kişilik bir sınıftan 1 başkan 20 farklı şekilde seçilir. Geriye kalan19 kişi arasından 1 başkan yardımcısı 19 farklı şekilde seçilir.
Buna göre, 1 başkan ve 1 başkan yardımcısı 20.19 = 380 farklı şekilde seçilir.
Yanıt B

7 kişi 4 kişilik sıraya kaç farklı şekilde sıralanır?
A) 120 B) 210 C) 360 D) 420 E) 840

1. sıraya: 7 kişiden biri
2. sıraya: 6 kişiden biri
3. sıraya: 5 kişiden biri
4. sıraya: 4 kişiden biri seçilir.
Buna göre, 7 kişi 4 kişilik sıraya
7.6.5.4 = 840 farklı şekilde sıralanır.
Yanıt E

8 öğrencinin katıldığı bir sınav başarı yönünden kaç farklı şekilde sonuçlanabilir?

1, 2, 4, 5, 6, 7 rakamları kullanılarak rakamları farklı dört basamaklı kaç farklı doğal sayı yazılır?
A) 480 B) 360 C) 240 D) 180 E) 120

Dört basamaklı bir doğal sayının binler basamağına 6 rakamdan biri yazılır. Rakamları farklı olduğundan, yüzler basamağına 5 rakamdan biri onlar basamağına 4 rakamdan biri birler basamağına 3 rakamdan biri yazılır.

[matematik_2_lys]