Özellik
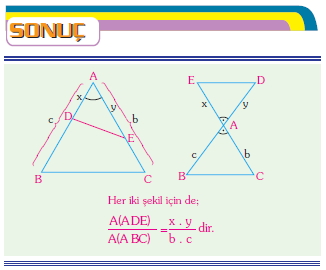
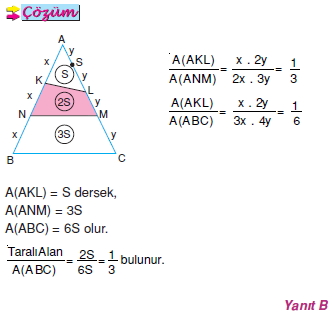
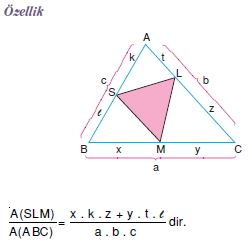
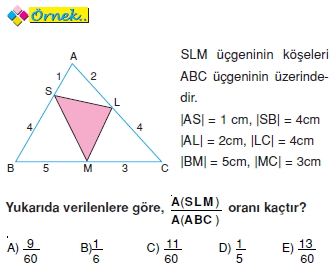
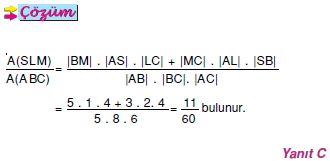
Bir üçgenin alanı iki kenar uzunluğu ile bu kenarlar arasındaki açının sinüsünün çarpımının yarısıdır.
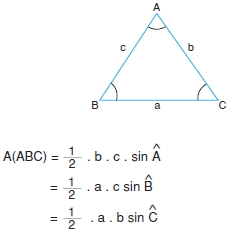

Özellik
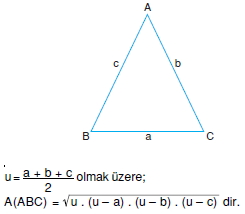
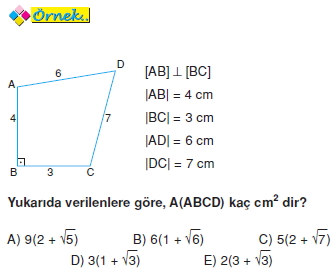
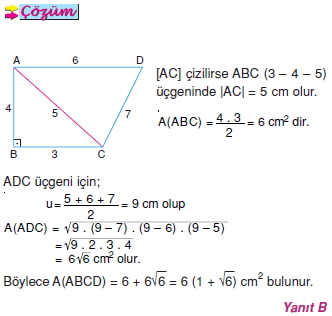
Kenar uzunlukları bilinen üçgenin alanı
Özellik
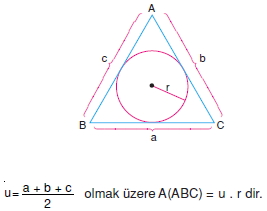
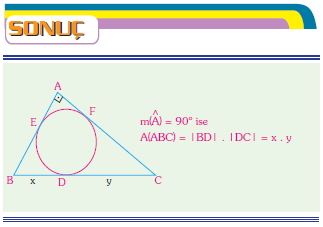
İç teğet çemberinin yarıçapı bilinen üçgenin alanı
Özellik
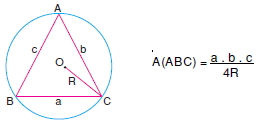
Çevrel çemberin yarıçapı bilinen üçgenin alanı

Özellik
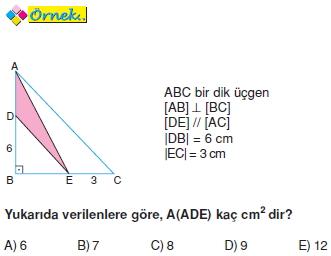
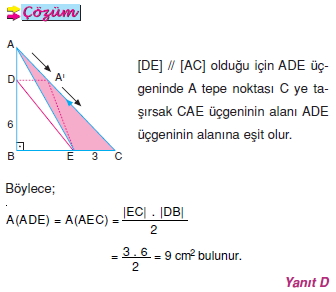
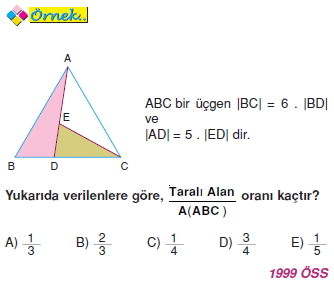
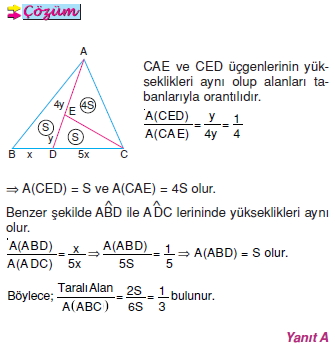
Yükseklikleri eşit olan üçgenlerin alanları tabanlarıyla orantılıdır.
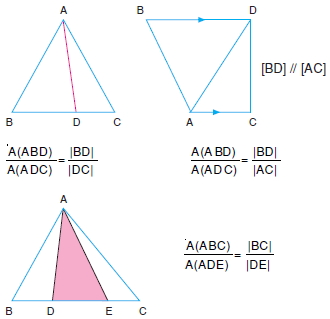
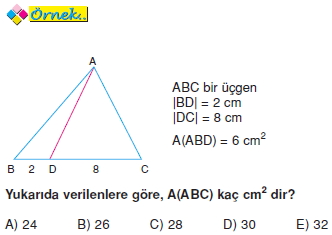
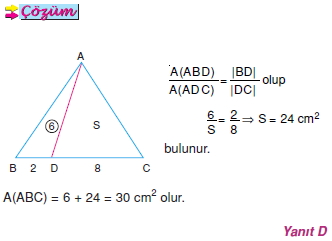
Özellik
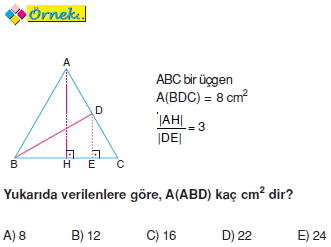
Tabanları eşit olan üçgenlerin alanları yükseklikleri ile orantılıdır.
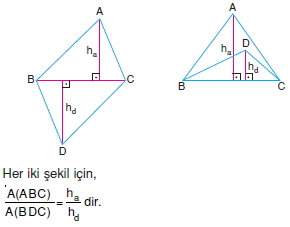
[ad1]
Özellik
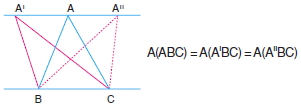
Taban uzunlukları ve yükseklikleri eşit olan ügenlerin alanları eşittir.

[m2]
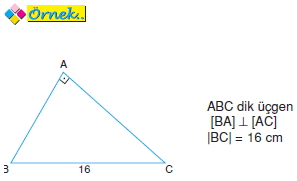
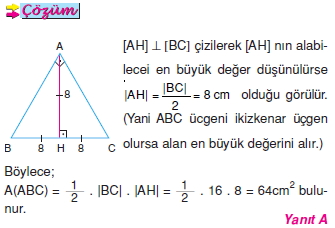
ABC dik üçgeninin alanının en büyük değeri kaç cm2 dir?
A) 64 B) 48 C) 32 D) 24 E) 16
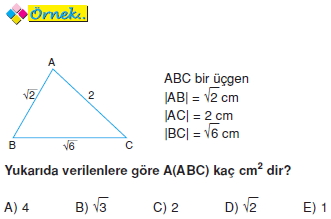
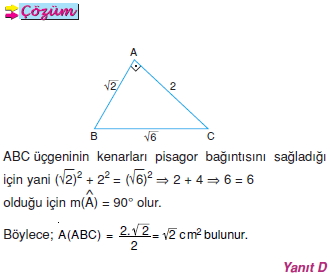
[geometri_ygs_lys]
